What is a time-constant spline?
When you use splines, generate points on the spline and the used increment between the points is constant you will get something like that: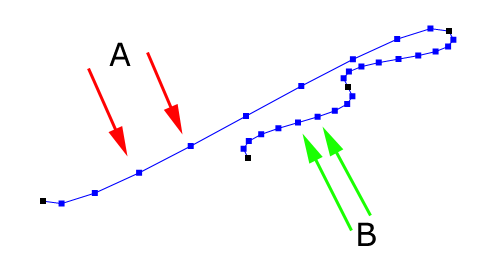
The distance between two points marked with red arrows (A) is another than the distance between the points marked with green arrows (B). Sometimes what you want to get is this:
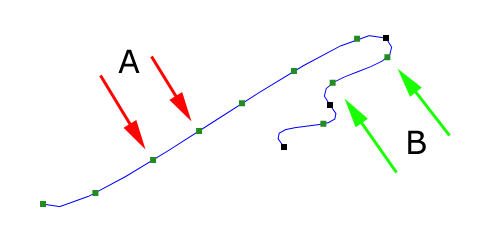
The distance between the points marked with red and green arrows is the same.
How is this done?
I've searched through the net, but most projects use a method where the spline is sampled and the sampled points are saved to calculate the distance traveled so far, and linear interpolation is used between two samplepoints. This works, but it's slow (you have to search through the sampledata to find the samplepoints) and waste lots of memory... But one idea from the net was different:Nils Pipenbrinck: I had to solve the same problem two days ago, and my solution - also it's just an approximation - works pretty good.
For each bezier curve I build a function that maps length to t (interplant).
First I sample the curve in 1000 steps to get the entire length and keep the sampled data. Then I normalize the data by dividing by the segment length. The data gets inverted in a way that I have a lookup table that maps length to t.
Then I fit a bezier to the data. I do least sqare error fitting (pretty easy) and I can throw away two of the 4 control points since the curve starts always at 0 and ends at 1. So in the end I have to store 3 additional floats per bezier: The segment length and the two control points of the length-to-t speed compensation bezier.
For a lookup I just have to normalize the "position" along the segment, do a bezier interpolation to get the interpolant and then pass this value to the 3d bezier.
The results are stunning! I tested it with all kinds of worst case bezier curves by moving an object along the path at constant speed, and I can't see *any* acceleration effects anymore, also I measured the error and it's still far from perfect. there are speed differences here and there, but there aren't any velocity leaps and the acceleration effects are so weak you won't notice them ever.
I do all the calculations during a data conversion step, so the time it takes to sample and approximate the bezier does not matter for the game. It just costs 3 floats per key (segment length + two tangents for speed compensation). The computational costs are neglible.. Just a hand full of muls and adds.
The Sources...
Here I've implemented Nils idea, where I've used the open-source least squares solver lmfit(also included in the source).
TimeConstSpline.zip